Лекция 9.
- §19. Логарифмический вычет.
- 1. Определение. Формула
подсчета числа нулей и полюсов
- 2. Теорема Руше и
основная теорема высшей алгебры
1. Определение. Формула
подсчета числа нулей и полюсов
Пусть f(z)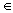 C
C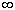 (
(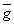 \z1,:zN),
zn- полюса и f(x )ч x
\z1,:zN),
zn- полюса и f(x )ч x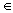

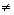 0. Тогда " x
0. Тогда " x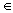
 - правильная и $ f(x )ч x
- правильная и $ f(x )ч x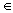
 .
.
Определение.
Функция j
(z)=f'(z)/f(z)=[ln f(z)]' называется логарифмической производной
функции f(z).
Вычеты j (z) в ее особых точках zn называются логарифмическими
вычетами.
Особыми точками
j (z) будут нули
z0k и полюса
zk функции f(z). Как считать
вычеты?
a) Пусть z0k - нуль порядка n функции f(z); =>
f(z)=(z-z0k)nf1(z),
f1(z0k)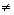 0 =>
0 =>
=> j
(z)=n/(z-z0k)+f'1(z)/f1(z) => Выч[j
(z),z0k]=n.
b) Пусть zk - полюс порядка p функции f(z);=> f(z)=y (z)/(z-zk)p , y (zk)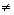 0
=>
0
=>
=> j (z)=-p/(z-zk)+ y '(z)/y (z) => Выч[j
(z),zk]=-p.
Теорема 19.1 Если
f(z)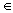 C
C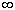 (
(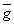 \z1,:zN),
zn- полюса и f(x )ч x
\z1,:zN),
zn- полюса и f(x )ч x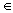

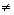 0, то
0, то 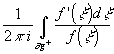 =N-P, где N- полное число нулей f(z) с
учетом кратности, P- полное число полюсов f(z) с учетом
кратности.
=N-P, где N- полное число нулей f(z) с
учетом кратности, P- полное число полюсов f(z) с учетом
кратности.
Доказательство. По основной теореме теории вычетов
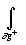 j (x )dx
=2p i
j (x )dx
=2p i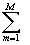 Выч[j
(z),zm]= 2p i[
Выч[j
(z),zm]= 2p i[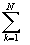 nk-
nk- pk]= 2p
i(N-P). n
pk]= 2p
i(N-P). n
В
частности, если f(z)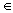 C
C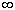 (
(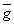 ), то N=
), то N=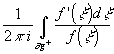 .
.
Принцип
аргумента. 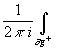 dlnf(x )=
dlnf(x )=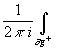 d ln|f(x )|+
d ln|f(x )|+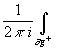 i d arg f(x ). Действительная функция
ln|f(x )| является
однозначной функцией, поэтому ее вариация (изменение) при обходе точкой
x замкнутого
контура
i d arg f(x ). Действительная функция
ln|f(x )| является
однозначной функцией, поэтому ее вариация (изменение) при обходе точкой
x замкнутого
контура  + равна 0. => Первое
слагаемое =0. Второе слагаемое представляет собой полную вариацию
arg(f(x )) при
обходе точкой x
замкнутого контура
+ равна 0. => Первое
слагаемое =0. Второе слагаемое представляет собой полную вариацию
arg(f(x )) при
обходе точкой x
замкнутого контура +, деленную на
2p . Итак,
N-P=(1/2p )Var[arg(f(x
))]|
+, деленную на
2p . Итак,
N-P=(1/2p )Var[arg(f(x
))]| + .
+ .
Геометрическая интерпретация. Изобразим
значения w=f(z) точками на комплексной плоскости w. Т.к. f(z)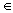 C(
C( ), то при полном обходе точкой z
контура
), то при полном обходе точкой z
контура  на
комплексной плоскости z, соответствующая ей точка на плоскости w описывает некий
замкнутый контур С. При этом точка w=0 может оказаться как вне, так и внутри
области, ограниченной контуром C. В первом случае Var[arg(w)]|С=0. Во
втором случае Var[arg(w)]|С= числу полных обходов вокруг точки w=0,
которое совершает точка w при своем движении по контуру C. При этом точка w
может обходить точку w=0 как в положительном направлении (против часовой
стрелки), так и в отрицательном (по часовой).
на
комплексной плоскости z, соответствующая ей точка на плоскости w описывает некий
замкнутый контур С. При этом точка w=0 может оказаться как вне, так и внутри
области, ограниченной контуром C. В первом случае Var[arg(w)]|С=0. Во
втором случае Var[arg(w)]|С= числу полных обходов вокруг точки w=0,
которое совершает точка w при своем движении по контуру C. При этом точка w
может обходить точку w=0 как в положительном направлении (против часовой
стрелки), так и в отрицательном (по часовой).
Принцип аргумента.
Разность между полным числом нулей и полюсов функции f(z) в области g
определяется числом оборотов, которое совершает очка w=f(z) вокруг точки w=0,
при положительном обходе точкой z контура  .
.
2. Теорема Руше и основная теорема высшей
алгебры
Теорема Руше Если f(z), j (z)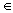 C
C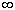 (
(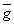 ) и |f(z)|
) и |f(z)| >|j (z)|
>|j (z)|  , то N[f+j
]g=N[f]g.
, то N[f+j
]g=N[f]g.
Доказательство. Для f(z) и F(z)=f(z)+j(z) выполнены все условия Теоремы
19.1 Действительно, f(z)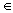 C
C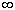 (
(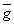 ) => f(z) |
) => f(z) | не имеет
особых точек и т.к.
не имеет
особых точек и т.к.
|f(z)| >|j (z)|
>|j (z)| =>|f(z)|
=>|f(z)|
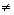 0.
0.
F(z)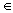 C
C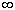 (
(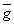 ) => F(z) |
) => F(z) | не имеет
особых точек и т.к. |F(z)|
не имеет
особых точек и т.к. |F(z)| =| f(z)+j (z)|
=| f(z)+j (z)|
 |f(z)|
|f(z)| - |j (z)|
- |j (z)| >0. =>N[f+j ]g=(1/2p )Var[arg(f+j )]
>0. =>N[f+j ]g=(1/2p )Var[arg(f+j )] ; N[f]g=(1/2p )Var[arg(f)]
; N[f]g=(1/2p )Var[arg(f)] ;
;
N[f+j
]g-N[f]g=(1/2p )Var[arg(f+j )- arg(f)] ={arg a-arg b=arg a/b т.к.
a=|a|eiarga, b=|b|eiargb=>
a/b=(|a|/|b|)ei(arg a-arg b)=> arg a/b = arg a-arg b
}=
={arg a-arg b=arg a/b т.к.
a=|a|eiarga, b=|b|eiargb=>
a/b=(|a|/|b|)ei(arg a-arg b)=> arg a/b = arg a-arg b
}=
=(1/2p )Var[arg((f+j )/f)] =(1/2p )Var[arg(1+j
/f)]|
=(1/2p )Var[arg(1+j
/f)]| . Введем функцию w=1+j /f. При обходе точкой z
контура
. Введем функцию w=1+j /f. При обходе точкой z
контура  соответствующая ей w опишет некоторую замкнутую кривую C, которая т.к.
|f(z)|
соответствующая ей w опишет некоторую замкнутую кривую C, которая т.к.
|f(z)| >|j (z)|
>|j (z)| целиком будет лежать внутри
некоторого круга |w-1|
целиком будет лежать внутри
некоторого круга |w-1| r <1, т.е. точка w=0 лежит
вне кривой С. => Var[arg(1+j/f)]|
r <1, т.е. точка w=0 лежит
вне кривой С. => Var[arg(1+j/f)]| =0 n .
=0 n .
Основная теорема высшей алгебры. Полином n-ой
степени имеет на комплексной плоскости ровно n нулей (с учетом их
кратности).
Доказательство. Представим полином
F(z)=a0zn+a1zn-1+:+an в виде F(z)=f(z)+j (z), где f(z)=a0zn, j (z)= a1zn-1+:+an. Составим отношение j
(z)/f(z)=(a1/a0)1/z+:+(an/a0)1/zn.
Для
" a0, a1,
an $ R0, что для "
|z|=R> R0 0<|j
(z)/f(z)||z|=R<1.
В силу Теоремы Руше
N[F] |z|=R= N[f] |z|=R. Но функция f(z)=a0zn на всей комплексной плоскости имеет единственный
n-кратный нуль- точку z=0.=> N[F] |z|=R= N[f]
|z|=R=n n

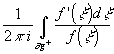 =N-P, где N- полное число нулей f(z) с
учетом кратности, P- полное число полюсов f(z) с учетом
кратности.
=N-P, где N- полное число нулей f(z) с
учетом кратности, P- полное число полюсов f(z) с учетом
кратности.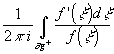 .
.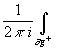 dlnf(x )=
dlnf(x )=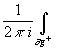 d ln|f(x )|+
d ln|f(x )|+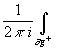 i d arg f(x ). Действительная функция
ln|f(x )| является
однозначной функцией, поэтому ее вариация (изменение) при обходе точкой
x замкнутого
контура
i d arg f(x ). Действительная функция
ln|f(x )| является
однозначной функцией, поэтому ее вариация (изменение) при обходе точкой
x замкнутого
контура