Лекция 9.
- §17.Понятие вычета аналитической функции
в изолированной особой точке.
- 1. Основная теорема теории вычетов.
- 2. Формулы вычисления Выч
[f(z),z0] в полюсе.
- 3. Вычет f(z) в z
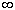
Пусть z0 - изолированная особая точка аналитической f(z).
f(z)=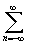 cn(z-z0)n;
0<|z-z0|< r, cn=
cn(z-z0)n;
0<|z-z0|< r, cn=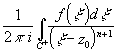 .
.
Определение .
Комплексное число Выч[f(z),z0]=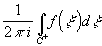 , где С
+ - замкнутый контур, который
можно стянуть к z 0 , оставаясь в
кольце аналитичности функции f(z)- называется вычетом f(z) в точке z 0.
, где С
+ - замкнутый контур, который
можно стянуть к z 0 , оставаясь в
кольце аналитичности функции f(z)- называется вычетом f(z) в точке z 0.
Очевидно Выч
[f(z),z0]=c-1.
1. Основная теорема теории
вычетов.
Основная теорема теории
вычетов. Пусть f(z)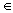 C
C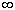 (
(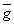 \z1,z2,...,zN)
за исключением конечного числа N изолированных особых точек. Тогда
\z1,z2,...,zN)
за исключением конечного числа N изолированных особых точек. Тогда  f(z)dz =2 p
i
f(z)dz =2 p
i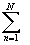 Выч
[f(z),zn].
Выч
[f(z),zn].
Доказательство. Если f(z)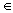 C
C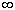 (
(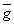 ), то
все точки
), то
все точки  - правильные точки f(z) . Выделим каждую из изолированных особых точек z
n функции f(z) замкнутым контуром
g n, не
содержащих внутри других особых точек, кроме z n. В замкнутой многосвязной области, ограниченной
- правильные точки f(z) . Выделим каждую из изолированных особых точек z
n функции f(z) замкнутым контуром
g n, не
содержащих внутри других особых точек, кроме z n. В замкнутой многосвязной области, ограниченной  и всеми контурами g n f(z) является всюду аналитической.
По теореме Коши для многосвязной области
и всеми контурами g n f(z) является всюду аналитической.
По теореме Коши для многосвязной области
 f(z)dz+
f(z)dz+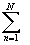
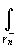 f(z)dz =0. Перенеся второе слагаемое направо, поменяв
направление обхода контуров, использовав определение вычета
получим искомое
f(z)dz =0. Перенеся второе слагаемое направо, поменяв
направление обхода контуров, использовав определение вычета
получим искомое  f(z)dz =2 p
i
f(z)dz =2 p
i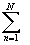 Выч
[f(z),zn]. n
Выч
[f(z),zn]. n
2. Формулы вычисления Выч
[f(z),z0] в полюсе.
Как считать вычеты?
a)
z0- устранимая особая точка . Выч
[f(z),z0]=0.
b) z0 - полюс порядка m>0
. f(z)=c-m/(z-z0)m+...+
c-1/z-z0+c0+... =>
=>
(z-z0)mf(z)= c-m+...+
c-1(z-z0)m-1+...=>
Выч
[f(z),z0]=c-1= .
.
Частный случай m=1. Выч [f(z),z0]=c-1=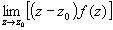 .
.
Если f(z)= j (z)/ y (z), j (z0)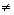 0, y
(z)=(z-z0) y '(z0)+...;
y '(z0)
0, y
(z)=(z-z0) y '(z0)+...;
y '(z0)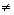 0.
0.
Тогда Выч [f(z),z0]=c-1=
j (z0)/ y
'(z0).
c) z0- существенно особая: Выч [f(z),z0]=
c-1=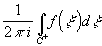
3. Вычет f(z) в z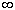
Вычет f(z) в
z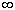 . Выч [f(z),z
. Выч [f(z),z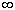 ]=-
]=-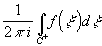 =-c-1. Если z
=-c-1. Если z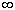 - устранимая особая точка, то вычет в ней может быть
отличен от 0.
- устранимая особая точка, то вычет в ней может быть
отличен от 0.
Пример.
f(z)=1+1/z. z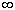 - устранимая особая точка , Выч [f(z),z
- устранимая особая точка , Выч [f(z),z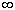 ]= -c-1=-1
]= -c-1=-1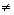 0.
0.
Сумма всех вычетов функции, аналитической на полной
комплексной плоскости, за исключением конечного числа изолированных особых
точек+ z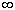 , включая вычет в z
, включая вычет в z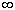 равна 0.
равна 0.
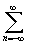 cn(z-z0)n;
0<|z-z0|< r, cn=
cn(z-z0)n;
0<|z-z0|< r, cn=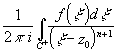 .
.