Лекция 9.
- §18. Вычисление несобственных интегралов
I-го рода от функции действительной переменной с помощью
вычетов.
- 1. Лемма 1. Теорема 1.
Примеры
- 2. Лемма 2 (Жордана). Теорема 2.
Примеры
1. Лемма 1. Теорема 1.
Примеры
Лемма 18.1 Пусть
f(z)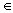 C
C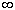 (|z|>R0
(|z|>R0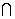 Imz>0), за исключением конечного числа изолированных особых точек и
|f(z)|<M/|z| 1+ d , d
>0. Тогда
Imz>0), за исключением конечного числа изолированных особых точек и
|f(z)|<M/|z| 1+ d , d
>0. Тогда 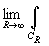 f( x =0.
f( x =0.
(C'R - полуокружность |z|=R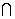 Imz>0).
Imz>0).
Доказательство.
При R>R0: |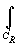 f( x
)d x |
f( x
)d x |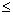
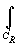 |f( x
)|ds<M p R/R1+ d
= M p /R d
|f( x
)|ds<M p R/R1+ d
= M p /R d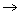 0 при R
0 при R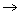
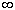 n .
n .
Замечания.
1.
Если условия Леммы 18.1 выполнены при j
1<arg z< j 2 ,
то 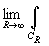 f( x )d
x =0.
f( x )d
x =0.
(C'R - дуга окружности, лежащая в
данном секторе: |z|=R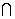 ( j
1<arg z< j
2))
( j
1<arg z< j
2))
2. Условия Леммы 18.1 будут
выполнены, если f(z) является аналитической в окрестности z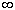 , которая является нулем не
ниже второго порядка для f(z).
, которая является нулем не
ниже второго порядка для f(z).
Теорема
18.1. Пусть f(x) задана при -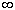 <x<
<x<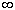 и $
аналитическое продолжение f(z) на Im z
и $
аналитическое продолжение f(z) на Im z 0, имеющее конечное
число изолированных особых точек z n , не имеющее особых точек на
действительной оси и удовлетворяющее условиям Леммы 18.1
. Тогда $ несобственный интеграл I-го
рода
0, имеющее конечное
число изолированных особых точек z n , не имеющее особых точек на
действительной оси и удовлетворяющее условиям Леммы 18.1
. Тогда $ несобственный интеграл I-го
рода  f(x)dx=2 p
i
f(x)dx=2 p
i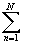 Выч[f(z),z
n].
Выч[f(z),z
n].
Доказательство. При R>R0 рассмотрим
замкнутый контур (-R<x<R)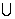 C'R{|z|=R
C'R{|z|=R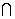 Imz>0}. По основной теореме теории вычетов
Imz>0}. По основной теореме теории вычетов
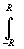 f(x)dx+
f(x)dx+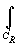 f( x )d
x =2 p i
f( x )d
x =2 p i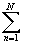 Выч[f(z),z n ]. Но, по
Лемме 18.1
Выч[f(z),z n ]. Но, по
Лемме 18.1 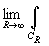 f( x )d x =0, правая часть не зависит от R =>
f( x )d x =0, правая часть не зависит от R =>
 f(x)dx=2 p i
f(x)dx=2 p i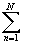 Выч[f(z),z n] n
.
Выч[f(z),z n] n
.
Замечания.
1. Если f(x)- четная
(f(-x)=f(x)) и удовлетворяет условиям Теоремы 18.1, то
 f(x)dx= p
i
f(x)dx= p
i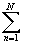 Выч[f(z),z
n]
Выч[f(z),z
n]
2. Имеет место аналогичная теорема, когда
аналитическое продолжение f(x) в нижнюю полуплоскость удовлетворяет условиям,
аналогичным условиям Леммы 18.1 для нижней
полуплоскости.
Пример.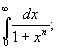 f(z)= f(z)=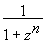 ; ; 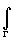 f(z)dz= f(z)dz=
=2 p iВыч[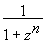 ,ei p /n]=(z0=ei p /n -полюс 1-порядка)= ,ei p /n]=(z0=ei p /n -полюс 1-порядка)=
=2 p i/(nei p (n-1)/n)=-2 p
i/(ne-i p /n ). С другой
стороны, |
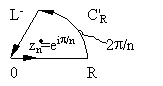
|
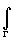 f(z)dz=
f(z)dz= f(z)dz+
f(z)dz+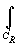 f( x )d
x +
f( x )d
x +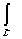 f(z)dz .При R
f(z)dz .При R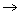
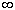 второе
слагаемое
второе
слагаемое 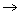 0
0
(по Замечанию 1 к Лемме 18.1 ) . В третьем слагаемом z=xe i2
p /n (f( xe i2 p
/n)=f(x)) . Устремив R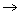
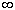 , получим
, получим  f(x)dx-ei2
p /n
f(x)dx-ei2
p /n f(x)dx=
(1-ei2 p /n)
f(x)dx=
(1-ei2 p /n) f(x)dx=-2 p
i/(ne-i p /n) =>
f(x)dx=-2 p
i/(ne-i p /n) => f(x)dx=-2 p
i/[(ne-i p /n) (1-ei2 p /n)]= p /(n sin p /n).
f(x)dx=-2 p
i/[(ne-i p /n) (1-ei2 p /n)]= p /(n sin p /n).
2. Лемма 2 (Жордана). Теорема 2.
Примеры
Лемма 18.2 (Жордана). Если f(z)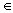 C
C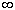 (|z|>R0
(|z|>R0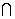 Imz>0) за исключением конечного числа изолированных особых точек и f(z)=>0
при |z|
Imz>0) за исключением конечного числа изолированных особых точек и f(z)=>0
при |z|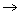
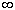 (равномерно по arg z,
(равномерно по arg z,
0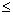 arg z
arg z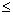 p ), z
p ), z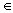 Imz>0, то при a>0
Imz>0, то при a>0 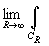 eia x
f( x )d x =0,
C'R - полуокружность
eia x
f( x )d x =0,
C'R - полуокружность
|z|=R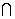 Imz>0.
Imz>0.
Доказательство . "e>
0 $ R : |f(z)|< e( R
) , |z|>R, причем e(
R )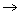 0 при R
0 при R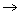
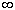 .
.
При R>R
0: |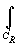 eia x
f( x )d x |
eia x
f( x )d x |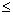
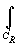 |eia x
f( x )|ds
|eia x
f( x )|ds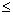
{ x
=Rei j =x+iy,x=Rcos j , y=Rsin j , ds=Rd
j , eia x
=eia(x+iy)= eiaxe-ay,
|eia x
|=e-ay=e-ay= =e-aRsin j }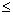 e R e R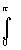 |eia x |d j = e R |eia x |d j = e R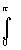 e-aRsin j d j =2
e R e-aRsin j d j =2
e R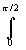 e-aRsin j d j< e-aRsin j d j< |

|
<{sin j (2/ p ) j при 0
(2/ p ) j при 0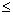 j
j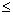 p /2}<2 e
R
p /2}<2 e
R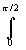 e-aR(2/ p
) j d j = pe (1-e-aR)/a
e-aR(2/ p
) j d j = pe (1-e-aR)/a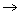 0 при R
0 при R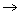
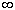 ,
,
т.к. e( R )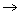 0 при R
0 при R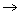
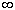 (a>0)
n .
(a>0)
n .
Замечания.
1 Если f(z) удовлетворяет условиям Леммы Жордана при Imz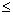 0,
0,
то при a<0 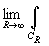 eia x
f( x )d x =0,
C'R - полуокружность |z|=R
eia x
f( x )d x =0,
C'R - полуокружность |z|=R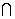 Imz<0.
Imz<0.
2. Если f(z) удовлетворяет условиям Леммы Жордана при Rez 0,
0,
то при a=i a ( a >0) 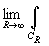 e- ax
f( x )d x =0,
C'R - полуокружность |z|=R
e- ax
f( x )d x =0,
C'R - полуокружность |z|=R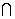 Rez>0.
Rez>0.
3. Если f(z) удовлетворяет условиям Леммы Жордана при Rez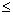 0,
0,
то при a=-i a ( a >0) 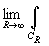 e ax
f( x )d x =0,
C'R - полуокружность |z|=R
e ax
f( x )d x =0,
C'R - полуокружность |z|=R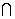 Rez<0.
Rez<0.
4. Лемма Жордана
остается справедливой, когда f(z) удовлетворяет условиям Леммы Жордана при Imz y0 (Rez
y0 (Rez x0; Imz
x0; Imz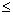 y0; Rez
y0; Rez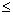 x0), y0
(x0 )- фиксированное число, которое может быть как >0, так и
<0, а интегрирование производится по дуге полуокружности |z-i y
0|=R
x0), y0
(x0 )- фиксированное число, которое может быть как >0, так и
<0, а интегрирование производится по дуге полуокружности |z-i y
0|=R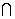 Imz>0 (|z-x0|=R
Imz>0 (|z-x0|=R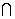 Imz>0; |z-i y0|=R
Imz>0; |z-i y0|=R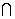 Imz<0; |z-x0|=R
Imz<0; |z-x0|=R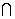 Imz<0). Доказательство аналогично, но
при оценке интеграла следует сделать замену x
=Rei j +iy0 ( x =Rei j
+x0).
Imz<0). Доказательство аналогично, но
при оценке интеграла следует сделать замену x
=Rei j +iy0 ( x =Rei j
+x0).
5. Лемма Жордана остается справедливой и при
ослабленных условиях на f(z). Пусть f(z) при Imz>y 0
при |z|>R0 , равномерно относительно arg(z-iy
1 ) при |z|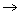
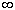 f(z)=>0 в
секторах - j 0
f(z)=>0 в
секторах - j 0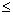 arg(z-iy1)
arg(z-iy1)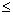 j
1, p - j
2
j
1, p - j
2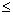 arg(z-iy1)
arg(z-iy1)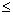 p + j 0 , и равномерно ограничена в секторе
j 1
p + j 0 , и равномерно ограничена в секторе
j 1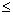 arg(z-iy1)
arg(z-iy1)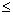 p - j 2 , где 0
p - j 2 , где 0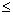 j 0, j 1,
j 2
j 0, j 1,
j 2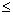 p
/2 и y 1>y0 . Тогда при a>0
p
/2 и y 1>y0 . Тогда при a>0
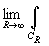 eia x
f( x )d x =0,
C'R - полуокружность |z-iy1|=R
eia x
f( x )d x =0,
C'R - полуокружность |z-iy1|=R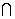 Imz>y0.
Imz>y0.
Теорема 18.2 Пусть f(x) задана при -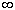 <x<
<x<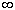 и $
аналитическое продолжение f(z) на Im z
и $
аналитическое продолжение f(z) на Im z 0, имеющее конечное
число изолированных особых точек z n , не имеющее особых точек
на действительной оси и удовлетворяющее условиям Леммы
Жордана . Тогда $
0, имеющее конечное
число изолированных особых точек z n , не имеющее особых точек
на действительной оси и удовлетворяющее условиям Леммы
Жордана . Тогда $ eiaxf(x)dx=2 p i
eiaxf(x)dx=2 p i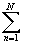 Выч[e iazf(z),zn ], где z
n - изолированные особые точки в верхней полуплоскости
Im z
Выч[e iazf(z),zn ], где z
n - изолированные особые точки в верхней полуплоскости
Im z 0.
0.
Доказательство. При R>R0 рассмотрим замкнутый
контур
(-R<x<R)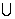 C'R{|z|=R
C'R{|z|=R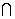 Imz>0}. По основной теореме теории
вычетов
Imz>0}. По основной теореме теории
вычетов
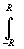 eiaxf(x)dx+
eiaxf(x)dx+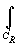 eia x
f( x )d x =2
p i
eia x
f( x )d x =2
p i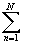 Выч[e
iazf(z),zn ]. Но, по Лемме Жордана
Выч[e
iazf(z),zn ]. Но, по Лемме Жордана
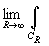 eia x f( x )d x
=0, правая часть не зависит от R =>
eia x f( x )d x
=0, правая часть не зависит от R =>
=> eiaxf(x)dx=2
p i
eiaxf(x)dx=2
p i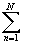 Выч[e
iazf(z),zn] n
.
Выч[e
iazf(z),zn] n
.
Пример. 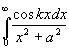 (k>0, a>0)=
(k>0, a>0)= =
= 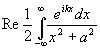 == Re p
iВыч[
== Re p
iВыч[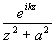 ,ia] =(z0 = ia
-полюс 1-порядка)= Re p i(e-ka/2ia)=
p e-ka/2a.
,ia] =(z0 = ia
-полюс 1-порядка)= Re p i(e-ka/2ia)=
p e-ka/2a.
Замечание. При
незначительном изменении формулировок Лемм 18.1 и 18.2 они остаются справедливыми и в случае бесконечного
числа изолированных особых точек f(z).
Определение . Функция комплексной переменной
f(z) называется мероморфной, если она определена на всей
комплексной плоскости и не имеет в конечной части плоскости особых точек,
отличных от полюсов.
Некоторые интегралы
1. 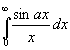 =sign(a) p
/2
=sign(a) p
/2
2. I= , 0<a<1; I=
, 0<a<1; I=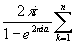 Выч[z
a-1f(z),zk]
Выч[z
a-1f(z),zk]
3. I= , 0<a<1; I=
, 0<a<1; I=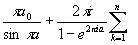 Выч[z
a-1(1-z)-af(z),zk], a0=
Выч[z
a-1(1-z)-af(z),zk], a0=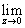 f(z).
f(z).
4.
I= f(x)ln(x)dx= p
i
f(x)ln(x)dx= p
i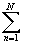 Выч[f(z)(lnz-i p /2),zk]
Выч[f(z)(lnz-i p /2),zk]
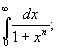 f(z)=
f(z)=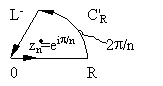
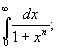 f(z)=
f(z)=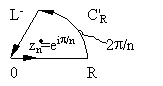

![]() <x<
<x<![]() и $
аналитическое продолжение f(z) на Im z
и $
аналитическое продолжение f(z) на Im z![]() 0, имеющее конечное
число изолированных особых точек z n , не имеющее особых точек
на действительной оси и удовлетворяющее условиям Леммы
Жордана . Тогда $
0, имеющее конечное
число изолированных особых точек z n , не имеющее особых точек
на действительной оси и удовлетворяющее условиям Леммы
Жордана . Тогда $![]() eiaxf(x)dx=2 p i
eiaxf(x)dx=2 p i![]() Выч[e iazf(z),zn ], где z
n - изолированные особые точки в верхней полуплоскости
Im z
Выч[e iazf(z),zn ], где z
n - изолированные особые точки в верхней полуплоскости
Im z![]() 0.
0.![]() C'R{|z|=R
C'R{|z|=R![]() Imz>0}. По основной теореме теории
вычетов
Imz>0}. По основной теореме теории
вычетов ![]() eiaxf(x)dx+
eiaxf(x)dx+![]() eia x
f( x )d x =2
p i
eia x
f( x )d x =2
p i![]() Выч[e
iazf(z),zn ]. Но, по Лемме Жордана
Выч[e
iazf(z),zn ]. Но, по Лемме Жордана
![]() eia x f( x )d x
=0, правая часть не зависит от R =>
eia x f( x )d x
=0, правая часть не зависит от R => ![]() eiaxf(x)dx=2
p i
eiaxf(x)dx=2
p i![]() Выч[e
iazf(z),zn] n
.
Выч[e
iazf(z),zn] n
.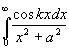 (k>0, a>0)=
(k>0, a>0)=![]() =
= ![]() == Re p
iВыч[
== Re p
iВыч[![]() ,ia] =(z0 = ia
-полюс 1-порядка)= Re p i(e-ka/2ia)=
p e-ka/2a.
,ia] =(z0 = ia
-полюс 1-порядка)= Re p i(e-ka/2ia)=
p e-ka/2a.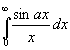 =sign(a) p
/2
=sign(a) p
/2 , 0<a<1; I=
, 0<a<1; I=![]() Выч[z
a-1f(z),zk]
Выч[z
a-1f(z),zk] , 0<a<1; I=
, 0<a<1; I=![]() Выч[z
a-1(1-z)-af(z),zk], a0=
Выч[z
a-1(1-z)-af(z),zk], a0=![]() f(z).
f(z).![]() f(x)ln(x)dx= p
i
f(x)ln(x)dx= p
i![]() Выч[f(z)(lnz-i p /2),zk]
Выч[f(z)(lnz-i p /2),zk]